Adrift map generation: WFC for rooms

In my last post on Adrift's map generation, I noted that the binary space partitioning technique that Adrift uses produces arbitrarily-sized rectangles for rooms. Generating the contents of rooms that aren't a standard shape is a bit of a challenge. Games like NetHack and Cogmind get around this by having very lightly-furnished rooms with 1-tile items. Brogue has a very interesting approach that helps it to produce "tactically interesting" rooms (Brian Walker gave an excellent talk about it at RogueCel 2018). In this post, I'll talk about one of the techniques Adrift uses to generate room contents: wave function collapse.

I'm not going to give a complete overview of the wave function collapse algorithm, because many others have done a great job of that already. If you haven't encountered the algorithm before, I'd recommend taking a moment to read a little about it and take a look at some of the things other folks have done with it. It's an impressively flexible algorithm!

Adrift uses a variation on the wave function collapse algorithm, implemented using a constraint solver, to generate different kinds of rooms in arbitrary shapes. These are the sorts of things it can produce:

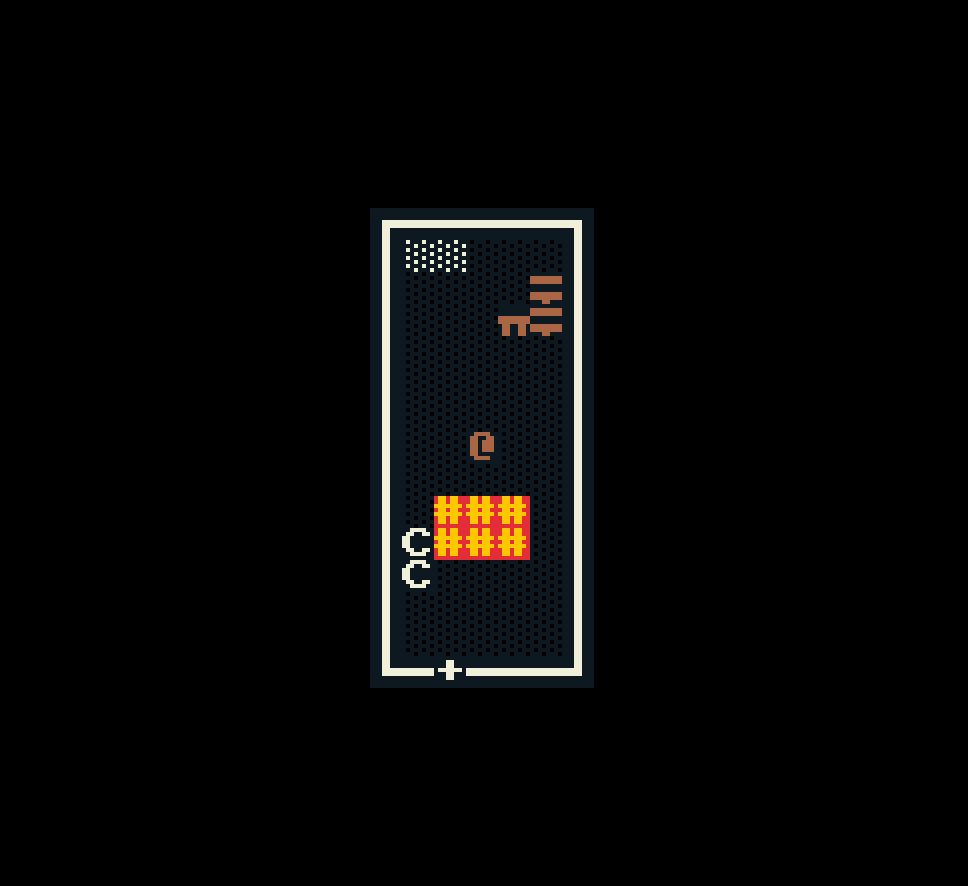
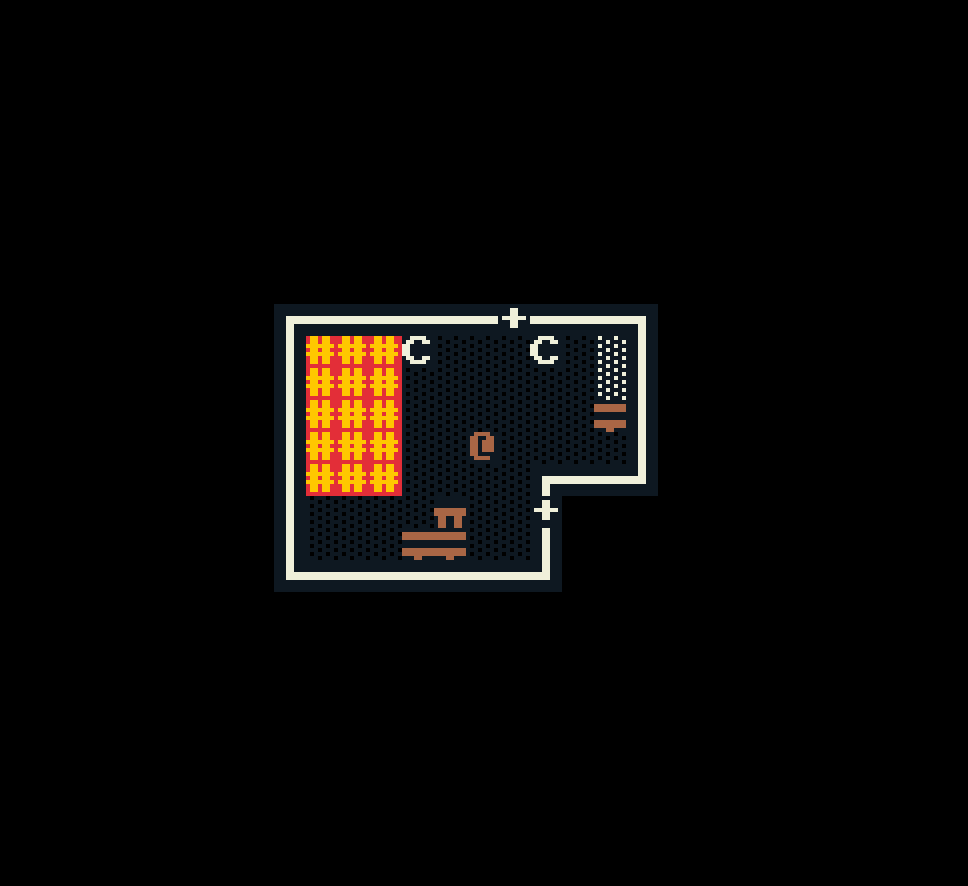
So far the space partitioning algorithm that generates the room boundaries always generates rectangles, but this approach for generating room contents can handle rooms of any shape.

So how does that work, then?

The idea is that each room is assembled by solving a jigsaw puzzle with a bunch of pieces of different sizes, where each piece can only match certain other pieces. So we have a bunch of jigsaw pieces with differently-shaped edges, and we try out placing them next to each other until we get an arrangement where all the edges match.

Each jigsaw piece defines a little chunk of the room that makes sense for the type of room being generated: in the break room, the pieces might be a couch, a table and chairs with a pack of cards, a TV by the wall, a bar with stools and a refrigerator. In the infirmary the pieces might be a gurney, a medicine cabinet, an oxygen tank, and so on. To assemble a room, all we have to do is solve the puzzle. Unlike a regular jigsaw puzzle though, there are many possible ways of connecting the pieces together. We're not aiming for a particular final room, just any arrangement of the pieces where the pieces fit together.

Adrift's architecture is heavily data-driven, and these room piece definitions are no different. For example, here's the current set of parts for the break rooms, snipped directly from the YAML data that drives the game:

- type: roomgen
  name: lounge
  algorithm: WFC
  options:
    parts:
      # empty space is allowed anywhere
      - |
        ***
        *.*
        ***

      # a sofa next to the wall
      - |
        xxxxx
        *hhh*
        *...*

      # a TV on the wall with some space next to it
      - |
        xxxxx
        *.D.*
        *...*

      # a bar with a refrigerator and some stools
      - |
        xxxxxxx
        *....R*
        *=====*
        *.s.s.*
        *.....*

      # chairs and tables
      - |
        *****
        *.c.*
        *.Tc*
        *...*
        *****
      - |
        *****
        *.c.*
        *.T.*
        *.c.*
        *****

      # heating vent
      - max: 1
        part: |
          xxx
          *V*
          *.*

      # replicator
      - max: 1
        part: |
          xxx
          *P*
          *.*

Each part defines a jigsaw piece. The characters around the edges of the piece define what will match there: x meaning the edge of the room, * meaning anything, and other characters matching those characters. So the first piece, a . with * surrounding it, is defining a 1x1 piece that can match anything on its four edges. The second piece, the sofa, is a 3x1 piece, and will only match the room's edge on its top side, and floor on its bottom side. The engine also automatically generates flipped and rotated versions of each piece, so the sofa could also appear on the left/right/bottom walls as well as the top.

The job of the room generator is to assemble these pieces into a room such that each piece is placed next to something that matches it, and every spot in the room is covered. For this, Adrift uses a constraint solver. If you're familiar with WFC, this is similar to the "simple tiled" model in WFC.

Wave Function Collapse is Constraint Solving

At its heart, the WFC algorithm is a simplified constraint solver. The vanilla WFC algorithm has no backtracking, though, and relies on an entropy-based heuristic to guide its search towards a satisfactory solution (i.e. one which has no mismatched edges between pieces). This is roughly similar to the "first-fail" heuristic which common in constraint solvers, where the solver chooses the next variable to try setting based on which has the smallest number of possible values remaining (proposed as early as 1965!). There's some subtlety in the way that noise is applied to entropy values in WFC that I have thus far ignored, but the results still seem pretty good even without taking that into account.

Formulating WFC as a constraint program and using a constraint solver rather than using a dedicated WFC algorithm gives us two advantages:

1. We get intelligent backtracking for free, and
2. We can impose generalized constraints on top of the inherent tile-adjacency constraints that WFC enforces.

You might have noticed the max: 1 annotation in the YAML above, which stipulates that at most 1 copy of that tile can be placed in the final room. (Adrift also supports a min count.) Vanilla WFC cannot accommodate this kind of constraint, but since we're using a full-blown constraint solver, it's relatively straightforward to add. I've also been able to add reachability constraints that prevent the solver from generating maps with unreachable sections. Adrift uses Choco as its constraint solver, though I also recommend or-tools for this kind of work—it has Python, C++ and Java bindings.

Constraint solvers only speak in integers, so in order to explain to the solver how to generate a map, we need to translate the task into its language. For generating rooms, we translate each cell in the grid as an integer variable with a range between 0 and n, where n is the number of possible ways a cell could be assigned (including rotation and flipping). So we have w ⨉ h integer variables. Then, we add in a constraint between each pair of horizontally adjacent variables, specifying the legal assignments of the pair. For example, if tile i can fit to the left of tile j, then (i, j) is a legal assignment of a pair of variables that are horizontally adjacent. Similarly for the vertically adjacent pairs. This tells the solver that it's only allowed to assign values to variables when they match their neighbors.

A note about the room pieces that are larger than 1x1: to explain these to the solver, we break each larger piece up into 1x1 sub-pieces, each of which can only match the appropriate sub-pieces from the same parent piece on its edges.

One of many

WFC, even with the additional power we get from using a full constraint solver, won't be a fit for every kind of room we want to generate in Adrift. That's why the data format allows for specifying different room generation algorithms, with options specific to the algorithm. In future, it might also turn out to be useful to be able to 'layer' room generation algorithms, first running WFC or another algorithm to generate the base furniture, and then running further algorithms to modify the results of the first algorithm—for example, adding trash to the room, or growing plants in it, or moving some of the furniture around.

That said, I've been happy with the quality and variety of the results so far, and I think there's a lot more I can get out of the algorithm by carefully authoring room pieces, and constraining it in interesting ways.