Or, How The Crap Do I Make That Curve?!
Sometimes I get an idea in my head that requires a particular kind of mathematical function: say, a cosine, or a logarithm, or a polynomial. Since I don’t have much of a background in mathematics, it’s more likely that I know the shape of function I want, but not how to write it down.
If I’m lucky, some dusty corner of my mind will shake off the cobwebs that have been accumulating there since first year algebra and offer itself in service, saying something useful like “Uh… maybe try tanh?”
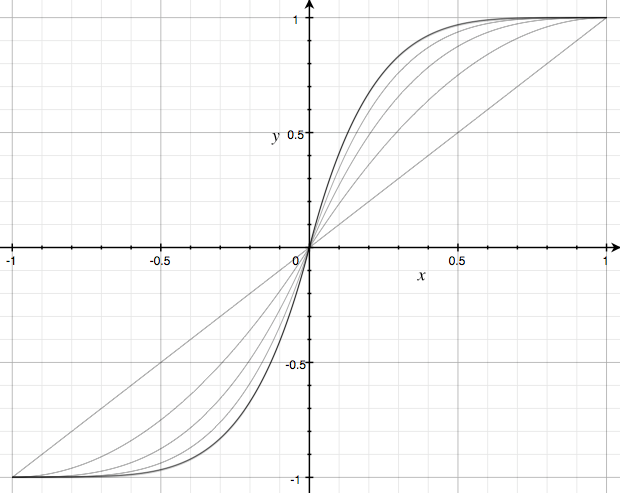
But today I was unlucky. I wanted something kind of like a square wave, but not as harsh. A sine wave was too smooth, and a square wave was not smooth enough. Surely there must be some mathematical incantation I can utter that will solve this problem! I had the idea that I wanted to start with a sine wave and “squash” it, so the bits between 0 and 1 were a bit closer to 1, and the bits between 0 and –1 were closer to –1.
My mathematical dust-gatherers had good intentions, saying things like “doesn’t squaring a number in [0,1] make it smaller, but in [1,∞) make it larger? Is that helpful?” and “doesn’t a sigmoid function look kind of like an S? Your curve has S-looking things in it, maybe a sigmoid would be useful.” But it turned out none of them had what I was looking for.
OK, so my math-rememberers weren’t working. Time to go to first principles. If I had some function squash(x), which pushed values in [-1,1] away from 0 and towards the edges of the range, what would its properties be? First, I know that squash(0) = 0. Also, squash(1) = 1 and squash(–1) = –1. And then some values in between: squash(0.5) should be a bit closer to 1, say 0.6. And squash(–0.5) should be a bit closer to –1, by the same amount as 0.5 got pushed towards 1. I plotted out the points just like in 9th-grade.
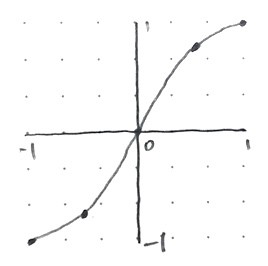
As I was looking at the picture I’d drawn, a lightbulb went off in my head: that looks kind of like Photoshop’s “curves” UI! A quick search and a helpful StackOverflow answer suggested Bezier splines, and from there I found cubic-bezier.com which let me draw some curves like I wanted, and also some curves that I didn’t want.
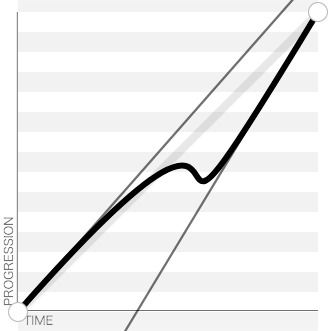
Some other pages had “ease-in-out” functions for quadratic, cubic, quartic and so on, but I wanted to be able to tune the sharpness of the curve all the way from a straight line (no squashing at all) to a square wave (squash everything < 0 to –1, and everything ≥ 0 to +1), smoothly. I wanted a parameter I could tune to say how sharp the curve was. I wanted cubic-and-a-half, or quartic-minus-a-bit.
I didn’t find the equation written down anywhere, so I figured it out. After a few dead ends, here’s what I came up with:
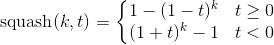
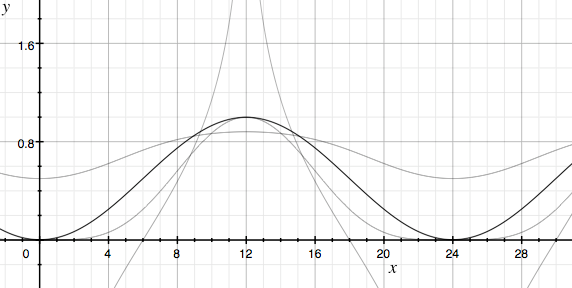
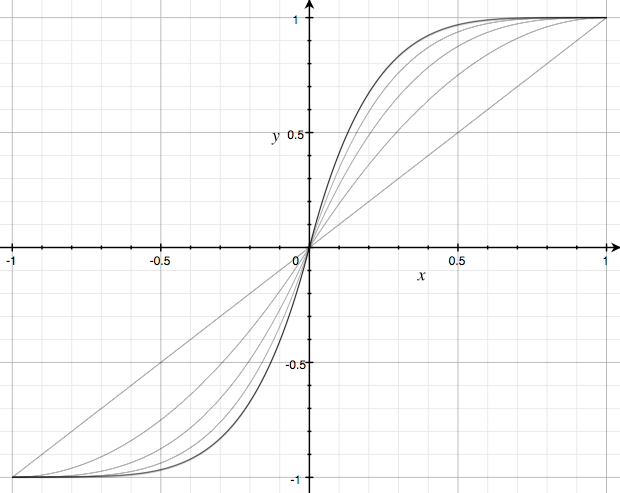
k here is the “squashedness” of the curve, where 1 is a straight line, and ∞ is a step function.
Feed the cosine into it, et voila!
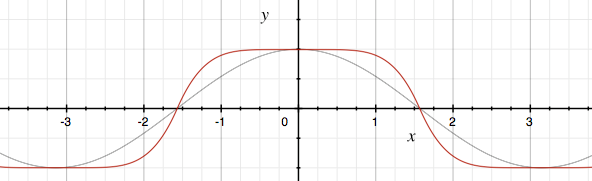
I can imagine this sort of function being useful for all kinds of things other than squashing cosines. You could run it over a generated terrain to make the cliffs harsher, and valleys wider, or use it in an animation to control “snappiness”. I’m going to use it to control light levels in a day-night cycle. If you use it, for making a game or otherwise, let me know on Twitter! I’m @nornagon there, you should follow me.